• Pravidla
• Zadania uloh domaceho kola
  • P-I-1
  • P-I-2
  • P-I-3
  • P-I-4

Matematicka olympiada je sutaz pre studentov strednych skol nasej republiky. Kategoria P je zamerana na programovanie a je urcena studentom vsetkych rocnikov.

Organizacia sutaze v kategorii P

Kategoria P matematickej olympiady ma tri postupove kola -- domace, krajske a celostatne.

V I. kole ucastnici riesia styri ulohy uvedene v tomto letaku. Riesenia odovzdaju svojmu ucitelovi informatiky do 9. novembra 2001. Ucitelia informatiky odoslu riesenia v tomto termine zo skoly na prislusnu adresu podla krajov takto:

Kosicky, Presovsky:
RNDr. G. Andrejkova, CSc.,
KMI PF UPJS,
Jesenna 5,
041 54 Kosice

Zilinsky:

RNDr. P. Varsa,
KI FRI Zilinska univerzita,
Moyzesova 20,
010 26 Zilina

Banskobystricky:

Mgr. L. Huraj,
KI FPV UMB,
Tajovskeho 40,
974 01 Banska Bystrica

Trnavsky, Trenciansky, Nitriansky:

Doc. Ing. V. Stoffova, CSc.,
KI FPV UKF,
tr. A. Hlinku 1,
949 74 Nitra

Bratislavsky:

RNDr. D. Pardubska, CSc.,
KVI FMFI UK,
Mlynska Dolina, 
842 48 Bratislava

Najuspesnejsi riesitelia domaceho kola su pozvani do II. kola (krajskeho), kde riesia styri teoreticke ulohy. Do III. kola (celostatneho) su pozyvani najuspesnejsi riesitelia vsetkych krajskych kol, pricom riesia tri teoreticke ulohy a dve prakticke ulohy pri pocitaci. Z najlepsich riesitelov tohto kola SK MO vyberie druzstva pre Medzinarodnu informaticku olympiadu a Stredoeuropsku informaticku olympiadu.

Predbezne terminy 51. rocnika MO kat. P

Usporiadatel sutaze

Matematicku olympiadu vyhlasuje Ministerstvo skolstva SR v spolupraci s Jednotou slovenskych matematikov a fyzikov a Slovenskou komisiou Matematickej olympiady. Sutaz organizuje Slovenska komisia MO a v jednotlivych krajoch ju riadia krajske komisie MO pri pobockach JSMF. Na jednotlivych skolach ju zaistuju ucitelia matematiky a informatiky. Celostatne kolo MO, tlac materialov MO a ich distribuciu po organizacnej stranke zabezpecuje IUVENTA - zariadenie pre volny cas deti, mladeze i dospelych MS SR v tesnej sucinnosti so slovenskou komisiou MO.

Formalna uprava riesenia

Popis riesenia.

Riesenia musia obsahovat podrobny popis pouziteho algoritmu, zdovodnenie jeho spravnosti a diskusiu o efektivite zvoleneho riesenia (t.j. posudenie casovych a pamatovych narokov programu). Algoritmus by mal byt jasny uz z popisu riesenia bez toho, aby bolo potrebne nahliadnut do programu.

Program.

V ulohach P-I-2 az P-I-4 je potrebne k rieseniu pripojit odladeny program napisany v jazyku Pascal, C alebo C++. Program sa odovzdava v pisomnej forme (jeho vypis je teda sucastou riesenia) i na diskete, aby bolo mozne otestovat jeho funkcnost. Subory na diskete pomenujte p1x.pas, p1x.cpp, kde x je cislo sutaznej ulohy. Disketu oznacte menom riesitela. Z jednej skoly mozno poslat vsetky riesenia na jednej diskete. V tomto pripade pre kazdeho riesitela vytvorte podadresar oznaceny jeho priezviskom a disketu oznacte adresou skoly. V ulohe P-I-1 je potrebne uviest dostatocne podrobny zapis algoritmu (najlepsie zdrojovy text najdolezitejsich casti programu, zo zapisu mozno vynechat jednoduche operacie ako su vstupy, vystupy, implementacie jednoduchych matematickych vztahov a pod.). V ulohe P-I-4b nakreslite pozadovanu komparatorovu siet.

Pisomnu cast riesenia vypracujte citatelne na listy formatu A4. Kazdu ulohu zacnite na novom liste a v zahlavi uvedte vase meno, triedu, adresu skoly a oznacenie prikladu podla tohto letaku. Zadania uloh nemusite opisovat. Ak sa vam riesenie nezmesti na jeden list, uvedte na dalsich listoch vlavo hore svoje meno a oznacenie ulohy a ocislujte strany.

KATEGORIA P

P-I-1

Uvazujme stvorcovu maticu A rozmerov n krat n, ktorej prvky su nuly a jednotky. Pod riadkovou resp. stlpcovou vymenou mame na mysli vymenu lubovolnych dvoch riadkov resp. lubovolnych dvoch stlpcov matice. V tejto ulohe sa zaujimame o to, ci je mozne postupnostou vymen transformovat maticu A na maticu, ktora ma na hlavnej diagonale iba jednotky (hlavnu diagonalu tvoria prvky A[1,1], A[2,2], ..., A[n,n]).

V mnohych aplikaciach (napr. riesenie sustav linearnych rovnic) je vyhodne danu maticu transformovat na ekvivalentnu maticu tak, aby hlavna diagonala obsahovala "velke" prvky. V tejto ulohe nuly reprezentuju "male" a jednotky "velke" prvky.

Sutazna uloha

Priklad:

Matica A: 0 1 0 1 1 1 0 1 1 1 0 0 0 0 1 0

Vysledok: 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1

Maticu mozno transformovat. Staci vymenit treti a stvrty riadok a potom prvy a stvrty stlpec.

Priklad:

Matica A: 0 1 0 1 1 0 1 1 0

Vysledok: Maticu nemozno transformovat.

P-I-2

Vo vyskumnom ustave potrubi a rur vyvinuli novy druh robota urceneho na cistenie teplovodnych potrubi. Robot sa sustavou rur pohybuje podla dopredu urceneho postupu. Technologia cistenia je taka, ze robot musi prejst kazdou rurou v sustave dvakrat (nezalezi ktorym smerom) - pri prvom prechode vykonava chemicke cistenie a pri druhom mechanicke docistovanie. Robot moze vojst do rury z lubovolneho konca, avsak ak raz vojde do rury, musi ju celu prejst.

Sustava rur pozostava z n uzlov ocislovanych od 1 po n, medzi ktorymi vedie m teplovodnych rur ocislovanych od 1 po m. Kazda rura vedie medzi dvojicou uzlov a nema ziadne odbocky alebo vetvenia. Medzi kazdou dvojicou uzlov vedie najviac jedna rura. Mozete predpokladat, ze sustava rur je suvisla, t.j. robot sa moze dostat na lubovolne miesto sustavy. Robot zacina v uzle cislo 1 a po skonceni cistenia sa musi opat do tohto uzla vratit.

Sutazna uloha

Format vstupu. Prvy riadok vstupneho suboru rury.in obsahuje dve kladne cele cisla n a m (n<=100), oddelene medzerou. Kazdy z nasledujucich m riadkov popisuje jednu ruru. Obsahuje dve cisla oddelene medzerou - koncove uzly rury.

Format vystupu. Vystupny subor rury.out pozostava z jedineho riadku, obsahujuceho 2m+1 cisel uzlov oddelenych medzerami v poradi, v akom ich ma robot navstivit na navrhovanej trase. Prve a posledne cislo na riadku musi byt 1. V pripade, ze neexistuje trasa, ktora prejde kazdu ruru prave dvakrat, vystupny subor bude obsahovat jediny riadok so slovom NIE. Ak existuje vhodnych tras viac, vypiste lubovolnu (jednu) z nich.

Priklad:

Subor rury.in 5 6 1 3 1 4 1 5 2 4 3 5 4 5

Subor rury.out 1 3 5 4 1 5 4 2 4 1 5 3 1

P-I-3

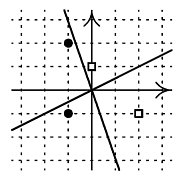
V rovine je danych 2n bodov, z toho n bielych a n ciernych. Spravodliva priamka je taka priamka, ktora:

• prechadza bodom [0,0],
• neprechadza ziadnym ciernym ani bielym bodom,
• rozdeluje rovinu na dve polroviny, pricom v jednej z tychto polrovin je rovnako bielych bodov, ako v druhej ciernych, a naopak.

Sutazna uloha

Mozete predpokladat, ze ziadne tri zadane body nelezia na jednej priamke, a ze bod [0,0] nelezi na ziadnej priamke urcenej dvoma zadanymi bodmi. Vsetky zadane body maju celociselne suradnice.

Format vstupu. Subor priamka.in na prvom riadku obsahuje cislo n. Kazdy z nasledujucich 2n riadkov obsahuje suradnice jedneho bodu oddelene medzerou. Prvych n bodov je bielych, druhych n bodov je ciernych.

Format vystupu. Subor priamka.out na prvom riadku obsahuje lubovolny bod rozny od [0,0], ktorym hladana spravodliva priamka prechadza. Suradnice oddelte medzerou. Ak spravodliva priamka pre danu mnozinu bodov neexistuje, vypiste do suboru slovo NIE.

Priklad:

Subor priamka.in 2 0 1 2 -1 -1 -1 -1 2 Subor priamka.out 2 1 Ine spravne riesenie -1.0 2.9

Pomocka: Nech A1=[x1,y1], A2=[x2,y2] a A3=[x3,y3] su body v rovine. Ak je hodnota (x2-x1)(y3-y1)-(x3-x1)(y2-y1) kladna, bod A3 lezi nalavo od polpriamky A1A2. Ak je tato hodnota zaporna, tak lezi napravo a ak je tato hodnota nulova, tak bod A3 lezi na priamke A1A2.

P-I-4

Komparatorove siete

Komparatorove siete sa vyuzivaju pri navrhu paralelnych algoritmov. Tiez je jednoduche ich realizovat pomocou elektronickych obvodov. Komparator je jednoduche zariadenie, ktore dostane na vstupe dve cisla, porovna ich a na vrchnom zo svojich vystupov vrati mensie z tychto dvoch cisel a na spodnom to vacsie. Z komparatorov mozno zostavit zlozitejsie obvody, ktore budeme volat komparatorove siete.

Komparatorova siet pozostava z n vodorovne usporiadanych vodicov, ktore su na niektorych miestach poprepajane komparatormi. Komparatory su usporiadane do vrstiev, ktore zodpovedaju krokom vypoctu. Na zaciatku vypoctu (v kroku 0) siet dostane na vstup n cisel. Po skonceni kroku k-1 sa vystupy z kroku k-1 prenesu vodicmi na komparatory vo vrstve k. Komparator vo vrstve k spaja vzdy dva vodice (nemusia byt susedne). Ak je na spodnom z nich mensia hodnota ako na vrchnom, vymeni tieto hodnoty, v opacnom pripade ich necha tak. V jednej vrstve moze byt aj viacero komparatorov (vypocet sa odohra naraz, paralelne), ale v jednej vrstve moze jeden vodic vstupovat najviac do jedneho komparatora. Po skonceni celeho vypoctu su na vystupoch siete tie iste cisla ako na vstupe, iba v zmenenom poradi.

Graficky sa vodice zobrazuju ako vodorovne ciary, komparatory ako zvisle spojnice svojich vstupnych vodicov. Komparatory v jednej vrstve sa kreslia zvislo nad seba, pripadne do niekolkych susediacich stlpcov. Jednotlive vrstvy oddelime ciarkovanou ciarou. Vypocet prebieha zlava doprava.

Pri navrhu sieti sa pokusame zostrojit ich tak, aby cas vypoctu bol co najmensi, t.j. aby siet mala co najmenej vrstiev. Druhym dolezitym kriteriom je pocet komparatorov (od tohoto poctu moze zavisiet napriklad cena vyroby siete).

Priklad.

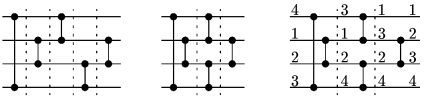
Uvazujme najlavejsiu siet na obrazku. Tato siet dostane styri vstupy a vrati ich utriedene od najmensieho po najvacsi. Po prvych dvoch krokoch vypoctu bude najmensi vstup bud na prvom alebo druhom vodici a najvacsi vstup na tretom alebo stvrtom. Dalsie dva kroky umiestnia najmensi a najvacsi prvok na ich miesto a v poslednom kroku dotriedime druhy a treti vodic. Vsimnite si, ze prvy a druhy komparator, podobne ako treti a stvrty, je mozno zlucit do jednej vrstvy bez toho, aby sa zmenil vysledok vypoctu. Vysledna rychlejsia siet je na prostrednom obrazku. Pravy obrazok ukazuje priebeh vypoctu pre vstup 4, 1, 2, 3.

Priklad. Zostrojte siet, ktora na vstupe dostane n cisel a na vystupe umiestni najmensie z tychto cisel na vodic 1 (na poradi ostatnych cisel nam nezalezi). Mozete predpokladat, ze n je mocnina dvoch.

Riesenie. Siet zostrojime rekurzivne. Oznacme S(n) siet, ktora ulohu riesi pre n vstupov. Ak n=1, S(n) nebude obsahovat ziaden komparator, lebo mame iba jeden vstup. Predpokladajme teda, ze n>1. Vstupy rozdelime na dve polovice (hornu a dolnu). Na kazdu polovicu aplikujeme siet S(n/2). Tieto dve siete polovicnej velkosti mozu pracovat paralelne. Po skonceni ich vypoctu mame na vodici 1 najmensi z hornej polovice vstupov a na vodici n/2 + 1 mame najmensi z dolnej polovice. Teraz staci pridat jeden komparator medzi vodicmi 1 a n/2 + 1 a dostaneme celkove minimum na prvom vodici. Siet S(n) teda pozostava z dvoch sieti S(n/2) a z jedneho komparatora. Konstrukcia siete S(n) je zobrazena na nasledujucom obrazku vlavo, vpravo je priklad vyslednej siete pre n=8.

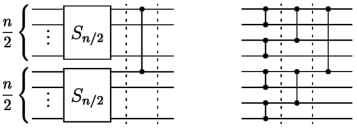
Vsimnime si, ze hlbka rekurzie je log₂ n, kedze velkost vstupu sa v kazdom rekurzivnom kroku znizi na polovicu. Kazda uroven rekurzie prida do vyslednej siete jednu vrstvu, preto siet S(n) ma log₂ n vrstiev. Pocet pouzitych komparatorov je v poslednej vrstve 1, v kazdej dalsej vrstve odzadu sa vzdy zdvojnasobi. Nech pocet vstupov je n=2^k. Potom pocet pouzitych komparatorov je 1+2+4+...+2^k-1=2^k-1=n-1 (sucet geometrickej postupnosti). Dostali sme teda siet, ktora ma O(log n) vrstiev a pouziva O(n) komparatorov.

Sutazne ulohy

a)

Napiste program, ktory bude simulovat komparatorove siete. Program vo vstupnom subore dostane komparatorovu siet a hodnoty vstupov. Navrhnite a popiste vlastny vstupny format pre zapis komparatovych sieti do suboru. Vas program by mal vypocitat vysledok vypoctu komparatorovej siete a tiez by mal umoznovat graficky alebo semigraficky zobrazovat priebeh vypoctu siete. Vo vasom rieseni uvedte aj priklady vstupu a vystupu z vasho programu.

b)

Na vstupe je n-1 cisel utriedenych od najmensieho po najvacsie (prvych n-1 vstupov). Posledny vstup obsahuje lubovolne cislo. Navrhnite komparatorovu siet, ktora zatriedi posledne cislo do tejto postupnosti (tzn. na vystupe bude vsetkych n cisel v utriedenom poradi). Mozete predpokladat, ze n je mocnina dvoch. Snazte sa, aby vasa siet bola co najrychlejsia.

This document was prepared with the help of the LaTeX2HTML translator Version 99.2beta6 (1.42)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.