Všetky rozumné distribúcie majú tento solver priamo vo svojom repozitári. Balíček, ktorý treba nainštalovať, sa väčšinou bude volať lp-solve alebo lp_solve.
Napr. v distrách používajúcich apt na správu balíčkov (napr. Debian, Ubuntu, Mint) vieš tento solver nainštalovať nasledovne:
sudo apt install lp-solve
(Ak náhodou nejaké distro tento balíček nemá, aktuálnu verziu si vieš vybrať a stiahnuť tu: https://github.com/lp-solve/lp_solve/releases/.)
Po nainštalovaní balíčku by malo ísť v príkazovom riadku spustiť binárku lp_solve.
Pre použitie pod Windows odporúčame stiahnuť priamo od autorov skompilovanú binárku lp_solve.
Aktuálnu verziu pre Win64 nájdeš tu: https://github.com/lp-solve/lp_solve/releases/download/5.5.2.14/lp_solve_5.5.2.14_exe_win64.zip.
Po stiahnutí a rozbalení dostaneme súbor lp_solve.exe, ktorý vieme spúšťať z príkazového riadku (cmd / powershell).
Vyrobíme si textový súbor nugetky.lp obsahujúci nasledovný text:
max: 6x_1 + 9x_2 + 20x_3; 200x_1 + 290x_2 + 610x_3 <= 3200; int x_1, x_2, x_3;
Z príkazového riadku spustíme solver:
lp_solve nugetky.lp
Dostaneme výstup:
Value of objective function: 102.00000000 Actual values of the variables: x_1 1 x_2 4 x_3 3
Program pre lp_solve musí obsahovať jednotlivé časti v presne tom poradí, v ktorom sú uvedené vyššie: najskôr definíciu cieľa, potom zoznam obmedzení a na záver (ak treba) deklaráciu typov premenných.
Pristavme sa ešte pri deklarácii typov premenných, teda pri riadku int x_1, x_2, x_3; vo vyššie uvedenom programe. Týmto riadkom hovoríme, že všetky naše premenné majú obsahovať nezáporné celé čísla. Prečo tento riadok treba uvádzať? Preto, že lp_solve vie riešiť nielen celočíselné lineárne programy ale aj všeličo iné podobné. (Schválne, skús si, aké riešenie nájde, ak tento riadok z programu vynecháš.)
Celú dokumentáciu ku lp_solve nájdeš napr. tu: https://web.mit.edu/lpsolve/doc/.
Syntax textového formátu vstupov, ktorý sme použili vyššie, nájdeš tu: https://web.mit.edu/lpsolve/doc/lp-format.htm.
Tu je príklad zadania sudoku (prevzatý z Wikipédie):
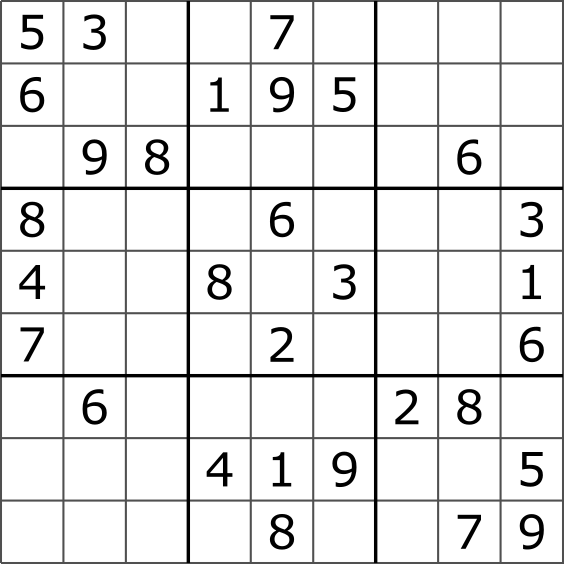
Tu je to isté sudoku ako textový súbor sudoku.txt:
5 3 . . 7 . . . . 6 . . 1 9 5 . . . . 9 8 . . . . 6 . 8 . . . 6 . . . 3 4 . . 8 . 3 . . 1 7 . . . 2 . . . 6 . 6 . . . . 2 8 . . . . 4 1 9 . . 5 . . . . 8 . . 7 9
Napíšeme si v bežnom programovacom jazyku program, ktorý vygeneruje podmienky zodpovedajúce pravidlám sudoku a potom načíta popis konkrétneho sudoku vo vyššie uvedenom textovom formáte a vypíše ďalšie podmienky zodpovedajúce jeho konkrétnemu zadaniu.
Príklad takéhoto programu v Pythone: sudoku_lp.py
Vygenerovaný lineárny program pre vyššie uvedený vstup: sudoku.lp
Spustíme solver. Všimni si prepínač -presolve. Presolving odporúčame pri lp_solve
používať vždy.
(Presolving heuristicky predspracuje lineárny program do potenciálne jednoduchšej
podoby: napr. premenné s fixnou hodnotou nahradí konštantami, zmaže obmedzenia, o ktorých vie
určiť, že sú zbytočné a podobne. Toto by v podstate nikdy nemalo uškodiť a v praxi to veľmi často
výrazne prospeje: predspracovaný program je väčšinou menší a jednoduchší a solver ho vyrieši
oveľa rýchlejšie.)
lp_solve -presolve sudoku.lp
Dostaneme niekoľko stoviek riadkov výstupu, ktoré nám hovoria, ktoré premenné sú nuly
a ktoré jednotky.
Príklad výstupu: sudoku.lpout
Z výstupu zostrojíme vyriešené sudoku tak, že vyberieme všetky premenné s hodnotou 1 a podľa nich vyplníme jednotlivé políčka riešenia.
Vyriešené sudoku:
5 3 4 6 7 8 9 1 2 6 7 2 1 9 5 3 4 8 1 9 8 3 4 2 5 6 7 8 5 9 7 6 1 4 2 3 4 2 6 8 5 3 7 9 1 7 1 3 9 2 4 8 5 6 9 6 1 5 3 7 2 8 4 2 8 7 4 1 9 6 3 5 3 4 5 2 8 6 1 7 9